자신이 투자하는 포트폴리오의 평균 투자수익률을 제대로 알아야 계좌를 불릴 수 있다. 산술평균 수익률과 기하평균 수익률의 차이를 이해하고 투자의 의사결정 과정에 녹아 있어야 비로소 복리로 장기투자 성과를 낼 수 있기 때문이다.

‘스노우볼은 아무나 굴릴 수 없다.’

우리가 투자할 때 참고하는 은행이나 증권사, 포털사이트에서 제시하는 펀드 수익률은 주로 직관적으로 이해하기 쉬운 산술평균 수익률로 표기돼 있다. 보통 산술평균 수익률이 기하평균 수익률보다 높기 때문에 수익률이 높아 보이는 착시효과도 있다. 그래서 산술평균 수익률로 표기된 상품을 예상 기대수익률로 착각하고 매수하는 경우가 많다.

반면, 기하평균 수익률은 펀드와 포트폴리오의 성적을 더 현실적으로 반영할 수 있다. 복리와 변동성의 개념이 반영돼 있기 때문이다. <펀드 A>가 2020년에는 20% 수익, 2021년에는 10%의 손실이 발생했다고 가정해보자. 산술평균 수익률로 계산하면 2년간 평균 10%의 수익률을 거뒀다고 생각할 수 있다. 그러나, 실제로 <펀드 A>에 2020년에 1억원을 투자했다면 2021년 말에 원금은 1억800만원으로 불어나 있을 것이다. 2년간 원금대비 수익률을 계산하면 8%에 그친다. 산술평균 수익률인 10%보다 실제 수익률이 작은 것을 알 수 있다. 만약 기하평균으로 수익률을 구했다면 정확하게 맞았을 것이다. 왜 이런 현상이 벌어지는 걸까?

평균을 구하는 방식에는 산술평균과 기하평균 두 가지가 있다.

산술평균(arithmetic mean) = N개의 변수를 모두 합한 후 N으로 나눈 값

기하평균(geometric mean) = N개의 변수를 모두 곱한 후 N으로 제곱근 한 값

산술평균 수익률은 산술평균해 산출한 수익률을 말하고, 기하평균 수익률은 수익률을 기하 평균해 산출한 수익률을 말한다. 산술평균 수익률은 각각의 수익률이 개별적으로 발생했다고 생각하고 산출해 평균한 기댓값이다. 이는 매 순간의 기대수익률을 의미한다. 대다수 사람이 직관적으로 받아들이기가 쉽다.

그러나 ‘독립적 시행’ 개념으로 수익률 계산을 해서 장기투자의 관점에서 볼 때 부정확한 측면이 있다. 투자는 한 번만 매매하고 그만하는 것이 아니고 독립적인 매매결과의 합도 아니며 사실은 종속된 사건들의 연속된 매매로 인한 결과의 곱에 가깝기 때문이다.

기하평균 수익률은 각각의 수익률을 연속적으로 이어 붙여서 발생한 결과라고 생각하고 도출한 평균값이다. 즉 ‘연속적’으로 투자할 때 장기적으로 기대할 수 있는 수익률이 얼마인지를 의미한다. 장기투자를 할 때 복리개념이 내포된 투자수익률 계산식이라고 할 수 있다. 변동성을 반영해서 정확한 계산이 가능하나 계산이 복잡하고 직관적이지 않다.

투자금을 두고 동전을 던져서 앞이 나오면 두 배를 벌고 뒤가 나오면 절반을 잃는 게임을 한다고 생각해보자. 기대수익률을 알아보기 위해 평균 수익률을 계산해보면 산술평균 수익률은 25%이고 기하평균 수익률은 0%다. 산술평균 수익률은 게임을 시행하는 독립된 단일순간의 기대수익률을 의미한다. 투자금이 얼마인지? 몇 번째 게임인지? 등은 중요하지 않다. 독립적인 게임이 시행되는 시점에서 기대수익률이 25%가 된다는 의미다. 매번 일정한 돈을 가지고 게임을 할 때 기대할 수 있는 수익률이다.

기하평균 수익률은 게임을 할 때 투자금을 재투자하면서 연속적으로 게임을 했을 때 장기적으로 기대할 수 있는 수익률이 얼마인지를 의미한다. 그래서 복리의 개념과 연관을 지어 생각할 수 있다. 처음 투자한 투자금으로 게임을 연속해서 할 때 기대할 수 있는 수익률이다. 산술평균은 계산하기 쉽고 이해하기도 쉽다. 하지만 기하평균 수익률이 복리의 개념을 더 잘 반영하고 변동성을 내포하여 계산하기 때문에 투자에 참고로 활용해야 한다.

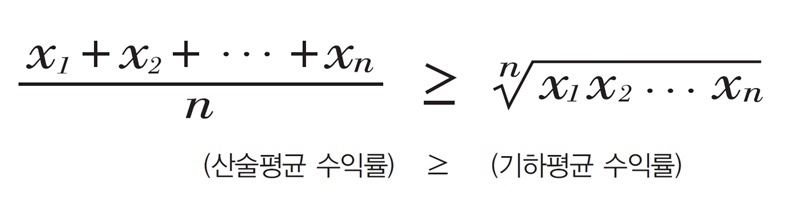
변동성이 없는 경우에는 산술평균 수익률과 기하평균 수익률이 같아진다. 하지만 대부분의 투자자산은 변동성을 가지고 있고, 이는 투자할 때 기대되는 기하평균 수익률이 산술평균 수익률보다 항상 작은 값을 갖게 되는 이유가 된다. 변동성이 심하면 산술평균 수익률은 양수인데 기하평균 수익률은 음수인 경우도 있다.

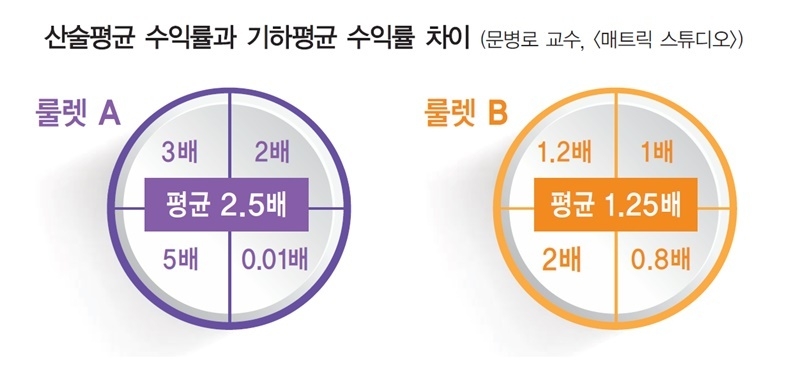
전에 언급했던 투자자가 1억원을 걸고 <룰렛 A>와 <룰렛 B>에 베팅을 해서 룰렛의 결과에 따라 투자 성과가 나는 게임을 예시로 들면 투자자가 1억원을 내고 1번만 룰렛을 돌릴 때는 <룰렛 A>를 선택하는 것이 2배는 유리하다.

기대수익률 (산술평균 수익률) = A (2억5,000만원) > B (1억2,500만원)

투자자가 1억원을 내고 4번을 연속해서 돌리는 게임을 할 때는 <룰렛 B>를 선택하는 것이 유리하다.

기대수익률 (기하평균 계산) = A (3,000만원) < B (1억9,000만원)

이런 결과는 <룰렛 A>와 <룰렛 B>의 산술평균 수익률과 기하평균 수익률의 차이 때문에 생긴다.

<룰렛 A>의 산술평균은 2.5, <룰렛 B>의 산술평균은 1.25이지만

<룰렛 A>의 기하평균은 0.74, <룰렛 B>의 기하평균은 1.18이다.

이렇게 연속된 매매를 이어가는 투자에는 예상되는 기하평균 수익률이 1이상이어야 장기투자 시 복리로 계좌가 불어나게 되는 것이다. <룰렛 A>처럼 기하평균 수익률이 1이하일 때 게임을 계속할수록 결과는 0에 수렴하게 된다.

기하평균 수익률을 높이려면 표준편차가 낮고 기대수익이 밀집돼 있어야 하고 그것은 변동성이 낮아야 함을 의미한다. 앞서 예시에서 <룰렛 A>가 <룰렛 B>보다 변동성이 큰 것을 상기하자. 특히 수익이 마이너스일 때 변동성이 커지므로 MDD(최대손실 폭)가 중요하다는 걸 알 수 있다. 그래서 저변동성에 낮은 MDD를 가진 포트폴리오를 만들려고 노력해야 예상되는 기하평균 수익률을 높일 수 있어 장기투자에 유리하다.

‘이제는 스노우볼을 굴릴 수 있다!’

보통의 개인투자자들은 로그함수인 기하평균보다 산술평균 수익률을 더 직관적으로 받아들이기 때문에 산술평균 수익률만 보고 <룰렛 A>를 연속해서 고르는 투자를 하기 쉽다.

투자라는 게 하루 이틀 하는 것도 아니고 한두 번 투자한 결과만 가지고 결론이 나는 것도 아닌데 대부분 투자자는 예상되는 산술평균 수익률이 높은 ‘개별주식’을 ‘남의 말에 따라’ 투자하기가 일쑤고 ‘큰 거 한방’에 변동성이 큰 투자(룰렛 A)를 반복적으로 시행한다면 계좌의 상태가 어떻게 될 건지는 수학적으로 명백한 것이다.

항상 포트폴리오의 변동성을 낮추려는 노력이 습관화돼 있어야 실전 투자에서 장기적으로 유의미한 결과를 얻을 수 있다. 포트폴리오의 변동성을 낮추는 여러 방법 중에서 분산투자가 있다. 다음 연재에서는 마지막으로 ‘베팅률의 조정’으로 어떻게 포트폴리오의 변동성을 낮출 수 있는지 알아보겠다.